第四章 正则表达式回溯法原理

学习正则表达式,是需要懂点匹配原理的。

而研究匹配原理时,有两个字出现的频率比较高: "回溯"

内容包括

• 没有回溯的匹配

• 有回溯的匹配

• 常见的回溯模式

没有回溯的匹配

假设我们的正则是 /ab{1,3}c,其可视化形式是:

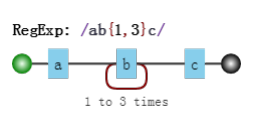
而当目标字符串是"abbbc"时候,就没有所谓的'回溯',其匹配过程是:

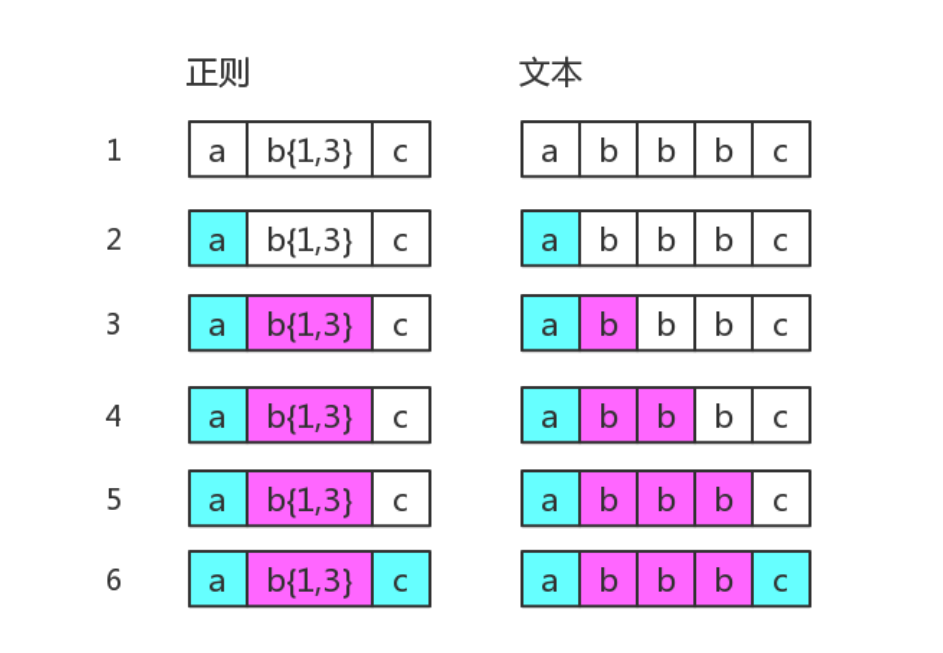
其中子表达式b{1,3}表示'b'字符连续出现 1 到 3 次

有回溯的匹配

如果目标字符串是abbc,中间就有回溯

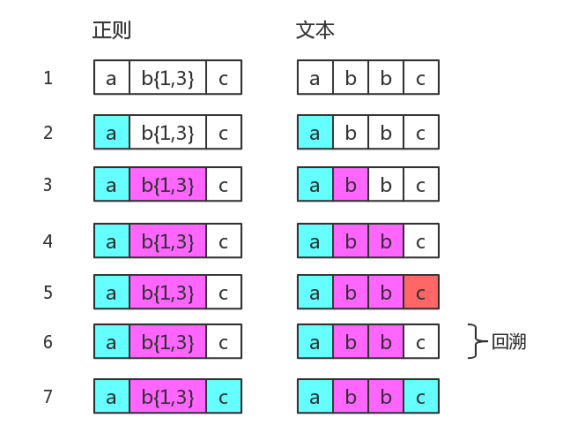
图中第 5 步有红颜色，表示匹配不成功。

此时 b{1,3} 已经匹配到了 2 个字符 "b"，准备尝试第三个时，结果发现接下来的字符是 "c"。那么就认为 b{1,3} 就已经匹配完毕。

然后状态又回到之前的状态（即第 6 步与第 4 步一样），最后再用子表达式 c，去匹配字符 "c"。当然，此时整个表达式匹配成功了。

图中的第 6 步，就是“回溯”。

这里再看一个清晰的回溯

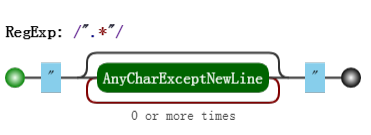
目标字符串是 "abc"de,其匹配过程是:

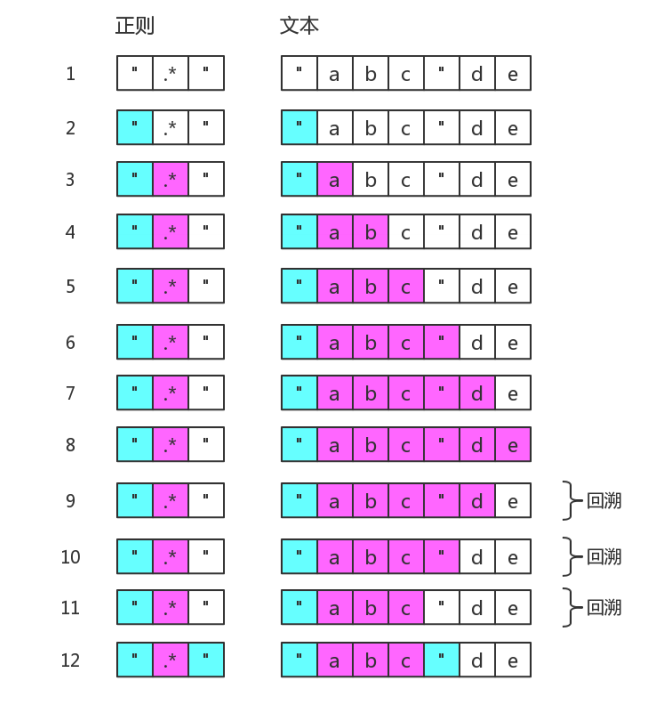
图中省略了尝试匹配双引号失败的过程,可以看出.*非常影响效率

为了减少一些不必要的回溯，可以把正则修改为 /"[^"]*"/。

常见的回溯形式

正则表达式匹配字符串的这种形式,有个学名,叫回溯法.

回溯法也称试探法，它的基本思想是：从问题的某一种状态（初始状态）出发，搜索从这种状态出发所能达到的所有“状态”，当一条路走到“尽头”的时候（不能再前进），再后退一步或若干步，从另一种可能“状态”出发，继续搜索，直到所有的“路径”（状态）都试探过。这种不断“前进”、不断“回溯”寻找解的方法，就称作“回溯法”。

本质上 就是深度优先搜索算法。其中推到之前的某一步这个过程,我们称之为回溯.从上面的描述中,我们可以看出,路走不通的时候,就会发生回溯.即 尝试匹配失败的时候.接下来的一步就是回溯

贪婪量词

之前的例子都是贪婪量词相关的比如b{1,3}因为其是贪婪的,尝试可能的顺序从多往少的方向去尝试。首先会尝试bbb,然后在看整个正则是否能匹配。不能匹配的时候,吐出一个b,即在bb的基础上,在继续尝试。如果还不行,在吐出一个。再试。如果还不行,只能说明匹配失败了

虽然局部匹配是贪婪的，但也要满足整体能正确匹配。否则，皮之不存，毛将焉附？

此时我们不禁会问，如果当多个贪婪量词挨着存在，并相互有冲突时，此时会是怎样？

答案是，先下手为强！因为深度优先搜索。测试如下：

var string = "12345";
var regex = /(\d{1,3})(\d{1,3})/;
console.log(string.match(regex));
// => ["12345", "123", "45", index: 0, input: "12345"]

其中，前面的 \d{1,3} 匹配的是 "123"，后面的 \d{1,3} 匹配的是 "45"。

惰性量词

惰性量词就是在贪婪量词后面加个问号。表示尽可能少的匹配,比如:

var string = "12345";
var regex = /(\d{1,3}?)(\d{1,3})/;
console.log(string.match(regex));
// => ["1234", "1", "234", index: 0, input: "12345"]

虽然惰性量词不贪，但也会有回溯的现象。比如正则是：

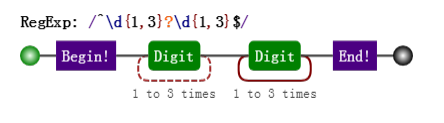
目标字符串是 "12345"，匹配过程是：

知道你不贪、很知足，但是为了整体匹配成，没办法，也只能给你多塞点了。因此最后 \d{1,3}? 匹配的字符是 "12"，是两个数字，而不是一个。

分支结构

我们知道分支也是惰性的，比如 /can|candy/，去匹配字符串 "candy"，得到的结果是 "can"，因为分支会一个一个尝试，如果前面的满足了，后面就不会再试验了。

分支结构，可能前面的子模式会形成了局部匹配，如果接下来表达式整体不匹配时，仍会继续尝试剩下的分支。这种尝试也可以看成一种回溯。

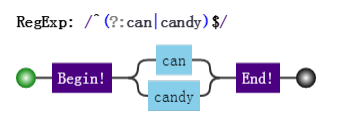
目标字符串是 "candy"，匹配过程

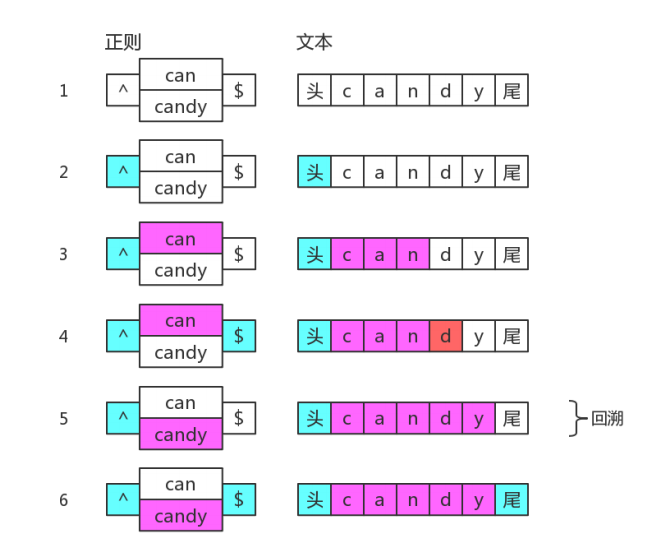
上面第 5 步，虽然没有回到之前的状态，但仍然回到了分支结构，尝试下一种可能。所以，可以认为它是一种回溯的。

总结

其实回溯法，很容易掌握的。

简单总结就是，正因为有多种可能，所以要一个一个试。直到，要么到某一步时，整体匹配成功了；要么最后都试完后，发现整体匹配不成功。

• 贪婪量词“试”的策略是：买衣服砍价。价钱太高了，便宜点，不行，再便宜点。

• 惰性量词“试”的策略是：卖东西加价。给少了，再多给点行不，还有点少啊，再给点。

• 分支结构“试”的策略是：货比三家。这家不行，换一家吧，还不行，再换。